Selamat belajar.
A. FLUKS MAGNET
 Fluks magnetik Φ didefinisikan sebagai jumlah garis gaya magnetik yang menembus tegak lurus suatu bidang kumparan. Berdasarkan operasi vektor, fluks magnetik didefinisikan sebagai perkalian skalar antara vektor induksi magnetik B dengan vektor luas bidang A. Besarnya fluks magnetik adalah : $\small \Phi =AB\cos \theta$
Fluks magnetik Φ didefinisikan sebagai jumlah garis gaya magnetik yang menembus tegak lurus suatu bidang kumparan. Berdasarkan operasi vektor, fluks magnetik didefinisikan sebagai perkalian skalar antara vektor induksi magnetik B dengan vektor luas bidang A. Besarnya fluks magnetik adalah : $\small \Phi =AB\cos \theta$ dimana:
Φ = fluks magnetik (Wb),
B = medan magnet (T);
N = garis normal
θ= sudut antara B dan N;
A = luas bidang ($m^{2}$)
B. GGL INDUKSI – HUKUM FARADAY
 Batang magnet di masukkan ke dalam kumparan, dan selama gerakan magnet batang jarum galvanometer menyimpang dari kedudukan semula.
Batang magnet di masukkan ke dalam kumparan, dan selama gerakan magnet batang jarum galvanometer menyimpang dari kedudukan semula.Pada saat magnet berhenti bergerak, jarum galvanometer kembali ke kedudukan semula. Pada saat magnet ditarik, jarum galvanometer menyimpang lagi dari kedudukan semula, tetapi arahnya berlawanan dengan pada saat magnet mendekati kumparan.
Ini menunjukkan bahwa dalam rangkain terjadi arus listrik (arus induksi) akibat beda tegangan yang disebut GGL induksi.
Hukum Faraday menyatakan bahwa : “ besar GGL induksi yang terjadi dalam kumparan berbanding lurus dengan cepat perubahan fluks magnetik yang dilingkupinya”. Jadi besarnya GGL induksi pada sebuah kumparan dengan N buah lilitan adalah : \begin{align*} \varepsilon = - N.\frac{d\Phi }{dt}= - N.A.\frac{dB }{dt}\end{align*}
N = banyak lilitan kumparan;
$\frac{d\Phi }{dt}$ = laju perubahan fluks magnetik
C. ARAH ARUS INDUKSI (HUKUM LENZ)
Hukum Lens berbunyi : “Arus induksi mengalir pada penghantar atau kumparan dengan arah berlawanan dengan gerakan yang menghasilkannya” atau “medan magnet yang ditimbulkannya melawan perubahan fluks magnet yang menimbulkannya”. Jika sebuah kawat lurus di gerakkan dengan kelajuan tertentu memotong medan magnet homogen, maka antara ujung-ujung penghantar timbul beda potensial yang disebut Gaya Gerak Listrik (GGL) induksi.
Jika sebuah kawat lurus di gerakkan dengan kelajuan tertentu memotong medan magnet homogen, maka antara ujung-ujung penghantar timbul beda potensial yang disebut Gaya Gerak Listrik (GGL) induksi.Jika ujung-ujung kawat dihubungkan sehingga terbentuk rangkaian tertutup, maka dalam kawat akan mengalir arus listrik yang disebut arus induksi. Jika kawat digerakkan dengan kecepatan v ke kanan dalam medan magnet B yang arahnya masuk bidang, maka timbul gaya Lorent ke kiri.sehingga arah arus listrik ke atas, seperti gambar.
Besarnya GGL induksi pada ujung-ujung kawat adalah :\[\varepsilon = B.L.v \sin \theta\] Pada kawat akan mengalir arus induksi yang besarnya :\[i=\frac{\varepsilon}{R}\]
$\epsilon$ =GGL induksi (Volt)
B = induksi magnet (T);
L = panjang kawat (m);
v = kecepatan gerak kawat (m/s)
i = arus induksi (A);
R = hambatan kawat ($\Omega$ = ohm);
$\theta$ = sudut antara v dan B
D. PENERAPAN INDUKSI ELEKTROMAGNETIK
1. Generator listrik
 Generator adalah alat untuk mengubah energi mekanik menjadi energi listrik. Generator ada dua jenis yaitu generator arus searah (DC) atau dynamo dan generator arus bolak-balik (AC) atau alternator.
Generator adalah alat untuk mengubah energi mekanik menjadi energi listrik. Generator ada dua jenis yaitu generator arus searah (DC) atau dynamo dan generator arus bolak-balik (AC) atau alternator.Generator bekerja berdasarkan prinsip induksi elektromagnetik yaitu dengan memutar suatu kumparan dalam medan magnet sehingga timbul GGL induksi.
Jika kumparan dengan N buah lilitan diputar dengan kecepatan sudut w, maka GGL induksi yang dihasilkan oleh generator adalah : \[\varepsilon =B.A.\omega .N.\sin \theta\] GGL induksi akan maksimum jika $\theta = 90^{o}$ atau $\sin \theta = 1$ , sehingga : \[\varepsilon_{max} =B.A.\omega .N\] sehingga persamaan di atas dapat ditulis menjadi:\[\varepsilon = \varepsilon_{max}\sin \theta\]$\varepsilon $ = GGL induksi (Volt);
$\varepsilon_{max} $= GGL induksi maksimum( volt) N = jumlah lilitan kumparan;
B = induksi magnet (T);
A=luas bidang kumparan(m) $\omega $ = kecepatan sudut kumparan (rad/s);
t = waktu (s);
$\theta = \omega .t $= sudut ($^{o}$)
2. Transformator
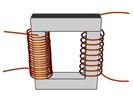 Transformator atau trafo merupakan alat untuk mengubah (memperbesar atau memperkecil) tegangan AC berdasarkan prinsip induksi elektromagnetik yaitu memindahkan energi listrik secara induksi melalui kumparan primer ke kumparan skunder.
Transformator atau trafo merupakan alat untuk mengubah (memperbesar atau memperkecil) tegangan AC berdasarkan prinsip induksi elektromagnetik yaitu memindahkan energi listrik secara induksi melalui kumparan primer ke kumparan skunder.Trafo menimbulkan GGL pada kumparan skunder karena medan magnet yang berubah-ubah akibat aliran arus listrik bolak-balik pada kumparan primer yang diinduksikan oleh besi lunak ke dalam kumparan skunder.
Trafo ada dua jenis, yaitu trafo step-up dan step-down. Trafo step-up berfungsi untuk menaikkan tegangan AC sumber, jumlah lilitan kumparan skunder lebih banyak dibandingkan jumlah lilitan primer.
Trafo step-down berfungsi untuk menurunkan tegangan AC sumber, jumlah lilitan skundernya lebih sedikit. Hubungan antara tegangan dan jumlah lilitan trafo adalah : \[\frac{V_{p}}{V_{s}}=\frac{N_{p}}{N_{s}}\] Efisiensi trafo besarnya dapat dihitung dengan persamaan :\[\eta =\frac{P_{s}}{P_{p}}=\frac{V_{s}I_{s}}{V_{p}I_{p}}\]Pada trafo ideal dengan efisiensi 100%, akan memiliki daya primer dan daya skunder yang sama besar. Jadi pada trafo ideal berlaku : \[P_{p}=P_{s}\\\frac{V_{p}}{V_{s}}=\frac{N_{p}}{N_{s}}=\frac{I_{s}}{I_{p}}\]$\eta $ = efisiensi trafo (%)
Vp = tegangan primer/input (Volt);
Vs = tegangan skunder/output (Volt) Np = tegangan primer;
Ns = tegangan skunder
Pp = daya primer (Watt);
Ps = daya skunder (Watt) Ip = kuat arus primer (A);
Is = kuat arus skunder (A)
3. Induktor
 Induktor merupakan kumparan yang memiliki banyak lilitan kawat. Induktor memiliki induktansi diri, yaitu gejala kelistrikan yang menyebabkan perubahan arus listrik pada kumparan dapat membangkitkan GGL induksi pada kumparan tersebut.
Induktor merupakan kumparan yang memiliki banyak lilitan kawat. Induktor memiliki induktansi diri, yaitu gejala kelistrikan yang menyebabkan perubahan arus listrik pada kumparan dapat membangkitkan GGL induksi pada kumparan tersebut.
Joseph Henry telah melakukan penyelidikan tentang ggl induksi akibat perubahan fluks magnetik yang ditimbulkan oleh suatu kumparan dan diperoleh kesimpulan bahwa besarnya GGL induksi sebanding dengan laju perubahan arus terhadap waktu.
Secara matematika pernyataan ini dapat dituliskan sebagai:\[\varepsilon = -L \frac{di}{dt}\] $\varepsilon $ = GGL induksi (Volt) $\frac{di}{dt}$ = laju perubahan kuat arus listrik (A) terhadap perubahan waktu (s)
Besarnya induktansi diri induktor sebesar : \[L=\frac{\mu _{o}A.N^{2}}{l}\]L = induktansi diri inductor (Henry = H);
N = jumlah lilitan inductor A = luas penampang inductor (ms);
$l$ = panjang inductor (m)
Induktor dapat menyimpan energi sebesar :\[W=\frac{1}{2}Li^{2}\]W = energi inductor (J); L = induktansi diri (H);
i = kuat arus listrik (A)
4. Induktansi Silang
Induktansi silang disebut juga induktansi timbal-balik, yaitu gejala kelistrikan akibat dua buah kumparan yang saling didekatkan. Jika salah satu kumparan mengalir arus listrik, maka akan timbul GGL induksi pada kumparan kedua.GGL induksi pada kumparan kedua menimbulkan medan magnet yang berubah-ubah, sehingga kembali menimbulkan GGL induksi pada kumparan pertama. Besarnya induktansi silang kedua kumparan adalah :\[L=\frac{\mu _{o}A.N_{1}N_{2}}{l}\]Besarnya GGL induksi pada umparan pertama dan kedua masing-masing adalah : \[\varepsilon _{1}= -M\frac{di_{2}}{dt} \hspace {5 mm} \\dan\\ \hspace {5 mm} \varepsilon _{2}= -M\frac{di_{1}}{dt}\]M = induktansi silang (H) $\mu _{o}$= permeabelitas ruang hampa N1 = jumlah lilitan kumparan pertama;
N = jumlah lilitan kumparan kedua
A = luas penampang kumparan;
$l$ = panjang kumparan (m)
I1 = kuat arus kumparan pertama (A);
I2 = kuat arus kumparan kedua (A)
Lanjut ke Soal dan Penyelesaian GGL Induksi
- Contoh Soal Dan Penyelesaian Ggl Induksi Kelas 12
- Contoh Soal Dan Penyelesaian Ggl Induksi Transformator
- 13 Soal Dan Penyelesaian Ggl Induksi Fisika UN
- 15 Soal Dan Penyelesaian Ggl Induksi Elektromagnetik







